Are you interested in making your money work for you? Do you want to know how much your savings can grow over time? Look no further! In this guide, we will explore the fascinating world of compound interest and provide you with a handy calculator formula to help you determine your future wealth.

What is Compound Interest?

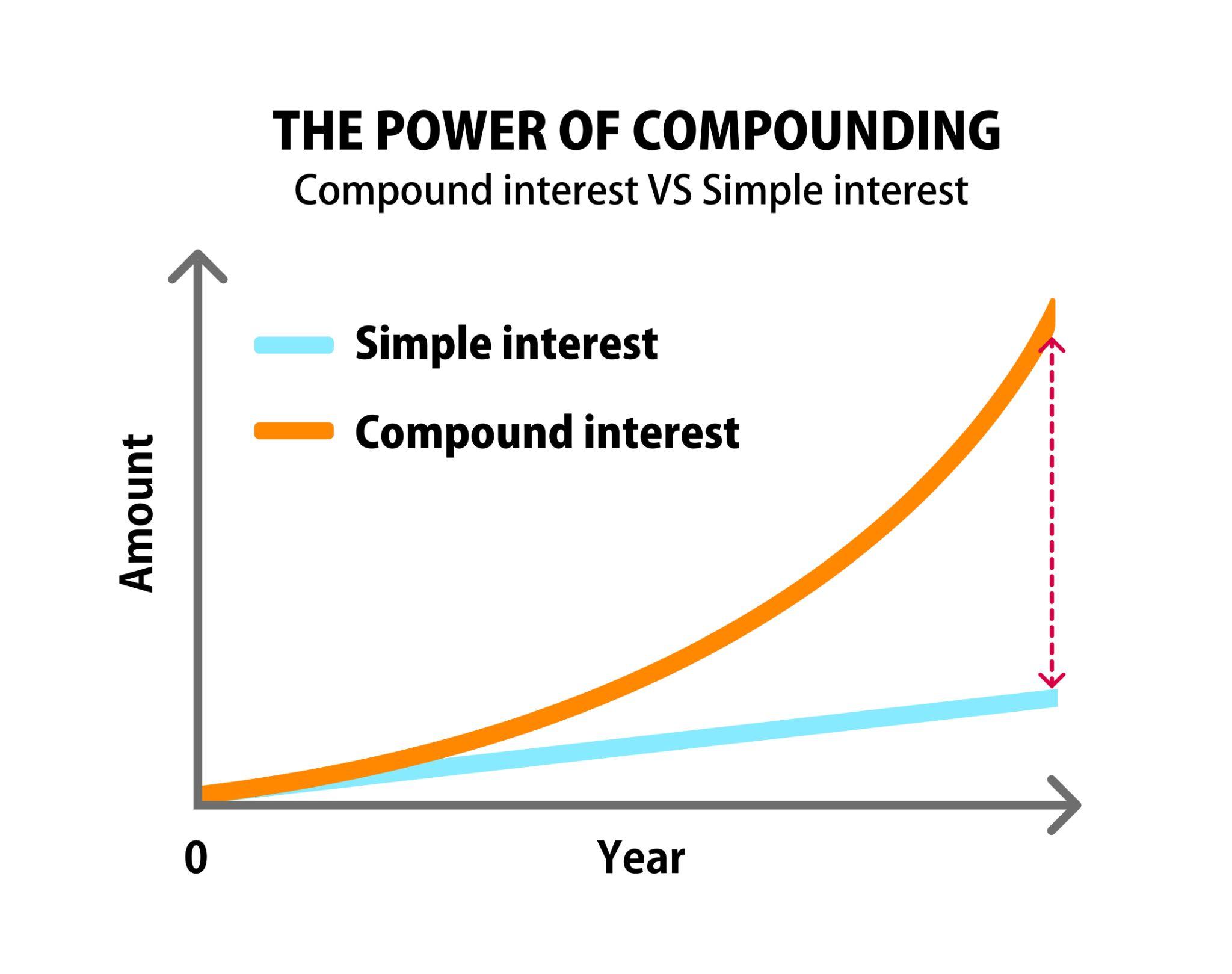
Compound interest is a powerful concept that allows your money to grow exponentially over time. Unlike simple interest, which is calculated only on the initial investment, compound interest also takes into account the accumulated interest. This means that your interest also earns interest, leading to a snowball effect that can significantly boost your savings.

The Formula

To calculate compound interest, you can use the following formula:

[A = P(1 + r/n)^(nt)]

Where:

• A is the future value of the investment/loan, including interest
• P is the principal amount (the initial investment/loan amount)
• r is the annual interest rate (expressed as a decimal)
• n is the number of times that interest is compounded per year
• t is the number of years the money is invested/borrowed for

How to Use the Calculator

Now that we have the formula, let’s put it into action with our compound interest calculator. Follow these steps:

1. Enter the principal amount (P): The initial investment or loan amount.
2. Enter the annual interest rate (r): This is the rate at which your investment or loan grows.
3. Enter the number of times interest is compounded per year (n): This could be yearly, quarterly, monthly, or even daily.
4. Enter the number of years the money is invested/borrowed for (t): The longer the investment period, the greater the impact of compound interest.

Once you have entered all the required information, our calculator will provide you with the future value of your investment or loan.

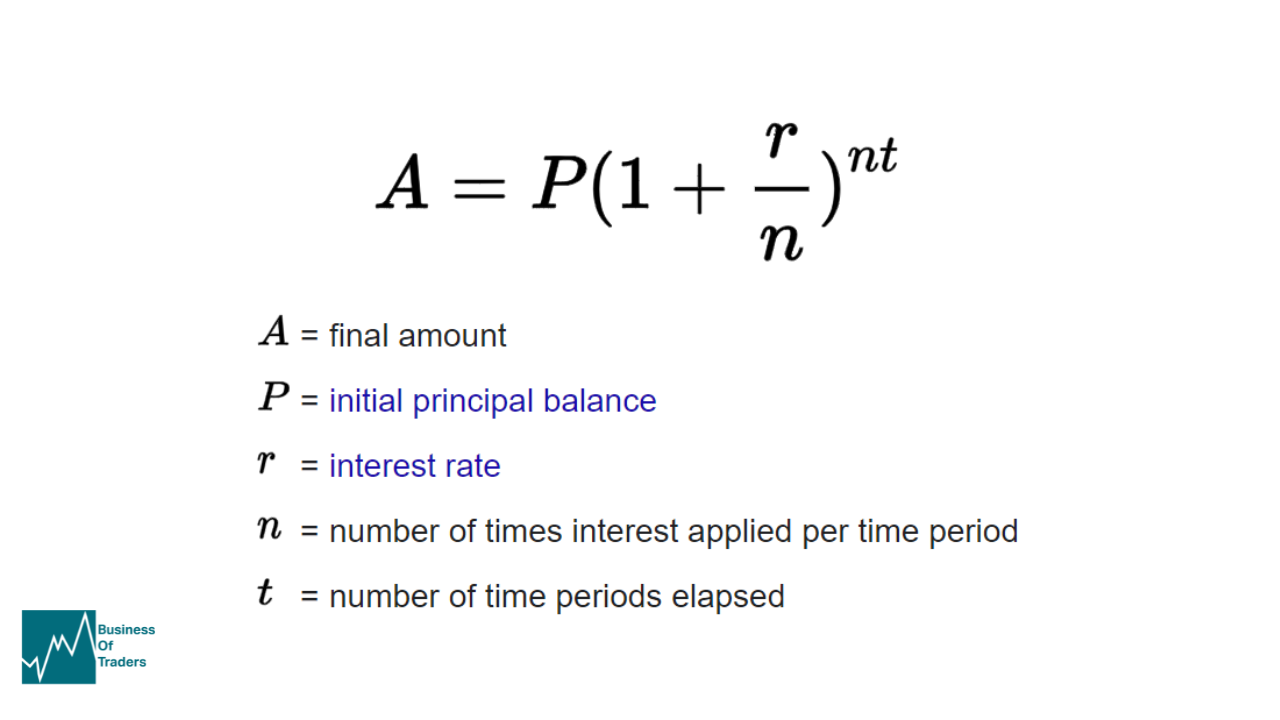
Example Scenario

Let’s say you have $10,000 to invest, and you want to know how much it will grow after 5 years with an annual interest rate of 5% compounded annually.

Using the compound interest formula:

[A = 10000(1 + 0.05/1)^(1*5)]

Calculating this equation, we find that the future value of your investment would be $12,763.81.

Internal Links: User Guide 

Simple Interest

Simple interest is a basic concept in finance that involves earning or paying interest on an initial investment or loan amount. Unlike compound interest, which takes into account the accumulated interest, simple interest is calculated only on the principal amount.

Formula for Simple Interest

The formula for calculating simple interest is:

[I = P \times r \times t]

Where:

• I represent the interest earned or paid
• P is the principal amount (the initial investment or loan amount)
• r is the annual interest rate (expressed as a decimal)
• t is the time period (in years) for which the interest is calculated

How Simple Interest Works

To understand how simple interest works, let’s consider an example:

Suppose you invest $1,000 in a savings account with an annual interest rate of 5% for 2 years. Using the simple interest formula, we can calculate the interest earned as follows:

[I = 1000 \times 0.05 \times 2]

The interest earned in this case would be $100.

Applications of Simple Interest

Simple interest is commonly used in various financial transactions, such as:

1. Loans: When you borrow money from a bank or other financial institution, the interest you pay is often calculated using simple interest.
2. Savings Accounts: Many savings accounts offer simple interest on the money you deposit, allowing your savings to grow over time.
3. Bonds: Bonds are debt securities that pay fixed interest over a specified period. The interest earned on bonds is typically calculated using simple interest.
   

   Pros and Cons

   Pros

   • Compound interest allows your money to grow exponentially over time, providing the potential for significant returns.
   • It can help you build wealth, reach financial goals, and secure a prosperous future.
   • Compound interest is a powerful tool for long-term investments, as the compounding effect can result in substantial growth.
   • It allows you to earn interest on both the initial investment and the accumulated interest, leading to higher returns compared to simple interest.
   • Compound interest applies to various investments and loans, including savings accounts, certificates of deposit, bonds, mortgages, and more.
   • By utilizing compound interest, you can optimize your financial strategies and maximize your returns.

   Cons

   • Compound interest assumes that the interest is reinvested and that there are no withdrawals or additional contributions. Any withdrawals or interruptions in the compounding process can affect the final results.
   • High interest rates and fees on loans can offset the benefits of compound interest, resulting in higher costs for borrowers.
   • Market fluctuations and inflation can impact the real value of the investment, especially if the interest rate is lower than the inflation rate.
   • Compound interest may not be suitable for short-term investments or loans that require flexibility.
   • It is important to consider the risks associated with investments and to diversify your portfolio to mitigate potential losses.

   It is important to carefully evaluate your financial situation and goals before making any investment or loan decisions. If you have specific questions or concerns, it is recommended to consult with a financial advisor.

Conclusion

Compound interest is a fantastic tool for growing your wealth. By understanding the formula and using our calculator, you can make informed financial decisions and watch your savings soar. Start investing today and harness the power of compound interest to secure a prosperous future!

Remember, the key to financial success is to start early and stay consistent. Happy investing!